Introduction

Mesurer, ou estimer la distance d’un objet très lointain est un problème difficile mais aussi fondamental en astronomie car nous n’avons accès qu’à une vision locale de l’Univers. Tous les objets visibles ne le sont pour nous que depuis la Terre ou son environnement proche.

Dès lors, tout paraît être positionné sur une sphère céleste qui entoure la Terre. Sur cette sphère il est assez facile de définir des distances entre les points, en particulier des distances angulaires. En revanche, savoir dire si un point est plus ou moins éloigné de nous, c’est beaucoup plus compliqué.

Plusieurs méthodes existent, et leur usage dépend en particulier de la distance qu’on veut mesurer. Lorsque cette distance est « assez » petite, on peut utiliser la méthode de la parallaxe. On verra que la limite d’usage de cette méthode dépend de la précision des instruments disponibles car en astrométrie il s’agit de mesurer des angles très petits, de très loin inférieurs à 1°.

C’est l’une des méthodes qu’utilise le satellite Gaia qui a permis d’établir une cartographie très précise des étoiles au voisinage du Soleil : voir l’article sur le site de l’IRAP

La parallaxe, de quoi s’agit-il ?

L’idée principale de cette méthode est d’observer le même objet mais vu de deux endroits différents.

Dans un premier temps, on observe un objet (par exemple une étoile), dans un repère connu, souvent par rapport à des étoiles beaucoup plus lointaines. On note avec précision la position de l’étoile, par exemple sa distance angulaire par rapport à une autre étoile de référence (très lointaine).

Puis on se déplace d’une distance D connue. Dans le cas de Gaia le déplacement est d’un diamètre d’orbite terrestre.

On observe alors à nouveau le même objet et on s’aperçoit qu’il n’est plus tout à fait à la même distance angulaire de notre étoile de référence.

Cette différence angulaire permet alors de calculer la parallaxe (la moitié de l’angle), qui, à partir de la distance D connue, suffit pour calculer la distance à laquelle se trouve notre objet.

Les deux schémas suivants illustrent ce principe :

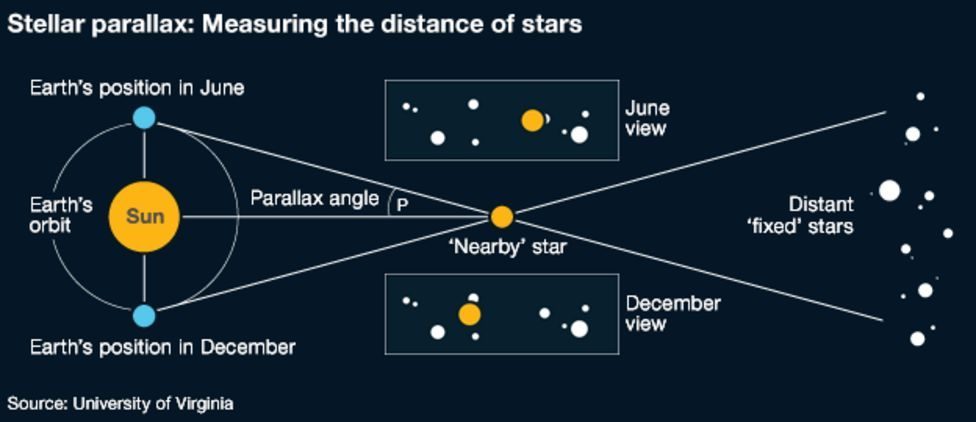
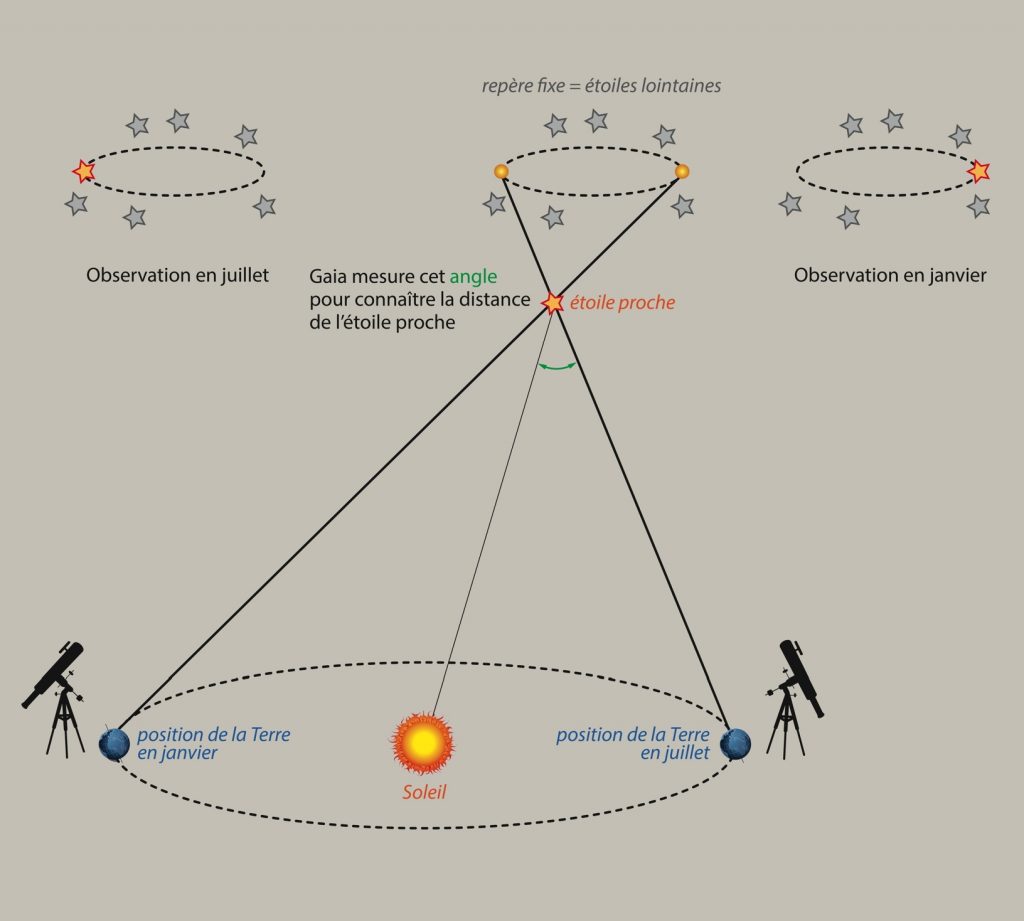
Le choix des étoiles de référence est assez délicat. Lorsqu’on observe depuis le sol, il faut tenir compte, dans l’incertitude, du fait qu’on ne peut que considérer que les étoiles lointaines sont immobiles, alors que dans l’espace, les satellites comme Gaia ou Hipparcos se basent sur des signaux en provenance d’objets très lointains, des quasars par exemple, dont le mouvement n’est pas mesurable même à la précision des instruments utilisés.

Application sur un exemple :

Pour illustrer ce principe, on remarque sur la carte du voisinage du Soleil que deux étoiles naines brunes Luhman 16A et Luhman 16B se situent à environ 2 parsecs du système solaire, c’est à dire 6,5 années-lumière.

Pour établir une distance approximative, on va se baser sur les informations disponibles dans la base de données SIMBAD (Set of Identifications, Measurements and Bibliography for Astronomical Data) consultable en ligne : Luhman 16.

On trouve alors une vue de ces étoiles, pas très spectaculaire, mais aussi d’autres informations très utiles comme celle qui nous occupe le plus : la parallaxe.

Dans SIMBAD on lit pour Luhman 16 :

Parallaxe      496 ± 37 mas (millisecondes d’arc, soit 1/3600000°)

Déterminons la distance alors pour ces étoiles :

En se basant sur le schéma de l’Université de Virginie, on définit D la distance à l’étoile, R la distance Terre-Soleil, p la parallaxe. On a alors :

R / D = tan(p) soit D = R / tan(p)

Si on prend R = 1 UA et p = 496.10^-3‘’ on a :

D = 1,4959787.10⁸ / tan (π / 180 x 496.10^-3 / 3600) = 6,2.10¹³km = 6,6 al

En tenant compte de l’incertitude sur la parallaxe on trouve entre 6,1 et 7,1al

On peut approximer tan(p) et p car l’angle est très petit et si on calcule :

D = 1,4959787.10⁸ / (π / 180 x 496.10^-3 / 3600) = 6,6 al

On obtient bien la même valeur.

La distance obtenue est donc 6,6 ± 0,5 al.

Comparons ce que nous avons obtenu avec la précision de Gaia :

Parallaxe      501,6 ± 0,1 mas (millisecondes d’arc, soit 1/3600000°)

On a alors :

D = 1,4959787.10⁸ / tan (π / 180 x 501,6.10^-3 / 3600) = 6,152.10¹³km = 6,502 al

En tenant compte de l’incertitude sur la parallaxe on trouve entre 6,501 et 6,504 al

La distance obtenue est donc 6,502 ± 0,002 al.

On remarque tout de suite la grande précision des informations produites par Gaia.

L’exemple développé ici peut être appliqué à toute autre étoile dont on peut obtenir la parallaxe dans SIMBAD ou dans le catalogue Gaia.

Limites de la technique

A travers l’exemple on s’aperçoit que les angles mesurés sont très faibles : 500 mas pour une distance de 6,5 al.

Pour se rendre compte de la prouesse technique que cela représente, un angle de 1 mas est à peu près l‘angle créé par un objet de 1 mm observé à 200 km de distance !

Or il y a bien des objets beaucoup, beaucoup plus lointains que les étoiles Luhman 16.

Une des limites va donc être dictée par la précision de l’appareil.

Mais pas seulement ! En effet, les performances dépendent aussi de la luminosité de l’objet observé ainsi que de son spectre lumineux.

En ce qui concerne Gaia, la précision annoncée pour l’astrométrie va de 0,01 mas pour des objets assez brillants (magnitude 13) à 0,8 mas pour des objets très peu brillants (magnitude supérieure à 20).

Or la luminosité apparente des objets dépend bien sûr de leur distance mais aussi de leur type et de leur taille. Il est donc très difficile de donner une limite précise pour cette technique.

On peut ainsi imaginer que la mesure donnée sera d’autant plus précise que l’objet est proche et lumineux.

Sauf qu’on se heurte à nouveau à d’autres problèmes. D’une part, si un objet est très proche, son mouvement propre modifiera plus rapidement les mesures d’angles effectuées et donc ajoute une incertitude sur la valeur obtenue. Par exemple, il est plus facile d’indiquer à une autre personne la position d’un avion passant loin dans le ciel plutôt que celle d’un oiseau passant à quelques dizaines de mètres. D’autre part, la quantité de lumière en provenance des objets très lumineux (soit parce qu’ils sont très proches, soit parce qu’ils sont plus lointains mais émettent plus de lumière) sature les détecteurs du satellite qui ne peut alors pas déterminer avec précision la position.

On peut aussi citer l’effet d’aberration de la lumière lié au déplacement relatif du détecteur par rapport à la source de lumière. C’est bien le cas car tout bouge dans l’Univers, et Gaia est en orbite avec un mouvement propre important et surtout périodique. On peut utiliser une métaphore pour expliquer ce phénomène : la lumière en provenance d’une étoile est remplacée par des gouttes de pluie tombant verticalement et le détecteur par le pare-brise d’une voiture. Lorsque la voiture est arrêtée, la direction de provenance de la pluie est bien la verticale. Mais quand la voiture roule, et plus sa vitesse est importante, plus la pluie semble provenir de l’avant. C’est exactement la même chose pour la lumière dont la vitesse de déplacement est finie et qui subit ce phénomène. Pour la précision des mesures il faut compenser la variation annuelle de cet effet qui peut atteindre 20 secondes d’arc.

Au final, les performances astrométriques de Gaia sont d’une précision meilleure que 0,1% pour la parallaxe de 100000 étoiles et de 10% pour 150 millions d’entre elles.

D’autres méthodes permettent d’estimer les distances d’étoiles plus lointaines : rien que dans la Voie Lactée on en estime le nombre à plus de 100 milliards !

Article réalisé avec l’aide de Pascal Fouqué, astronome à l’IRAP