Fiches documentaires
Notions de géodésie Enseignement supérieur Lycée

Étymologie
La géodésie (gé = Terre, daiôn = je divise) est la science de la forme et des dimensions de la Terre. Les questions de la de la forme de la Terre et de la définition du mètre sont très liées : pendant des siècles la définition du mètre était fondée sur la longueur d’un méridien terrestre.
Les enjeux de la géodésie
Connaitre la forme de la Terre, mesurer des distances entres différents points sur Terre, et définir des unités de longueur sont des préoccupations très anciennes et toujours d’actualité.
Les enjeux sont considérables et variés :
- stratégiques (militaire, politique, …)
- économiques (commerce, navigation, cartographie, …)
- technologiques (instruments de mesures : horloges, GPS, télémétrie laser, …)
- scientifiques (définition des repères de référence terrestres et célestes nécessaires pour connaitre la position précise d’objets sur Terre et dans l’espace : orientation/rotation de la Terre ; observation et compréhension du système terre et de son évolution : déformation tectonique, déplacement des masses d’eau ; …).
Anecdotes
- En 1999, échec de la mission Américaine Mars Climate Orbiter à cause d’une confusion entre unités métriques et anglo-saxonnes (https://fr.wikipedia.org/wiki/Mars_Climate_Orbiter).
- La « méridienne Verte » a été l’occasion de fêter le passage à l’an 2000 et de commémorer les expériences de mesure du méridien de Paris (https://fr.wikipedia.org/wiki/M%C3%A9ridien_de_Paris).
- La Terre n’est pas rigoureusement sphérique mais ellipsoïde. De ce fait, le plus haut point du globe en altitude – le Mont Everest – n’est pas le point le plus éloigné du centre de la Terre !
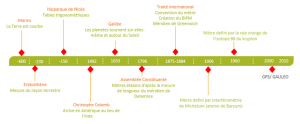
Quelques repères historiques sur les avancées en géodésie
Quelques méthodes pour mesurer des distances
La méthode de triangulation
Attribuée à Thalès de Milet (624-547 AEC), elle permet de déterminer des distances et donc des positions, connaissant des longueurs et des angles. L’intérêt est de positionner des points éloignés ou inaccessibles. C’est la technique mise en œuvre par Delambre pour mesurer la longueur du méridien, mais aussi par le satellite GAIA pour réaliser le catalogue des étoiles de notre Galaxie.
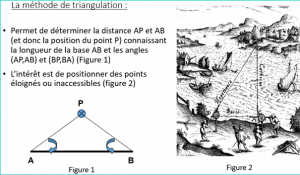
Figure 2 (cas particulier du triangle rectangle) : illustration tirée d’un livre de Levinius Hulsius, 1602
Exemple de la mesure de la circonférence terrestre par Eratosthène (vers 230 AEC)
Syène et Alexandrie ont pratiquement la même longitude. Il est midi (solaire) au même moment pour ces deux villes. Eratosthène observe qu’alors que le soleil éclaire le fond d’un puit à Syène, alors qu’un gnomon à Alexandrie projette une ombre. Si l’on suppose que les rayons du soleil sont parallèles, alors cela signifie que la Terre est courbe. De plus l’angle alpha mesuré au niveau du gnomon est égal à la différence de latitude entre les deux villes. En mesurant la distance qui sépare les deux villes (en comptant le nombre de pas), on peut en déduire le rayon de la Terre et donc sa circonférence.

Remarque : il s’agit ici d’une simplification, car les premières mesures étaient basées sur des arcs de cercle et non des angles.
La nécessité d’une unité de longueur commune
L’évolution des étalons de mesure
- Dès la plus haute antiquité en Asie et Egypte la coudée est utilisée comme étalon des mesures de longueur.
- Le pied, d’origine moins ancienne, était employé en général en Occident.
- En France, c’est la toise (égale à 6 pieds) qui était le plus souvent utilisée.
- Les étalons étaient précieusement conservés par les autorités. Mais ces étalons différaient d’un pays à l’autre et parfois même d’une région à l’autre.
- A la fin du XVIIIème siècle, la situation en France est particulièrement confuse, chaque seigneur utilisant ses propres unités. Les cahiers de doléance rédigés lors de la Révolution de 1789 réclamaient une mesure universelle. L’Assemblée nationale adopte alors la proposition de l’Académie des sciences d’une unité fondée sur la grandeur du méridien terrestre.
- La Terre devient le nouvel étalon (Universel) des mesures de longueur. La nouvelle unité est baptisée le mètre. Elle est égale à la dix-millionième partie du quart de méridien. Cette définition est purement conventionnelle. Selon cette définition, le périmètre méridien de la Terre est donc de 40 000 km exactement.

Illustration tirée de « Geometrei » de Jakob Köbel, 1575
La mesure du méridien par Delambre et Méchain
La nouvelle définition du mètre impose la mesure géodésique d’un arc de méridien. Entre 1792 et 1798, les deux astronomes Jean Baptiste Delambre et Pierre André Méchain mesurent l’arc du méridien de Paris depuis Dunkerque jusqu’à Barcelone. Ils utilisent la méthode de triangulation et le cercle répétiteur de Borda.
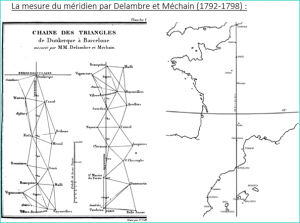
Illustration tirée de « Base du système métrique décimal » de Delambre et Méchain , 1806

Illustration tirée de « Astronomie populaire » de Arago, 1873
Les conventions internationales
- Une fois le mètre défini, c’est le système métrique décimal qui est institué en 1795 en France par la loi relative aux poids et mesures. Il s’agit d’un bouleversement majeur des pratiques humaines, la décimalisation introduisant une véritable révolution dans le calcul des surfaces et des volumes.
- Le système métrique décimal, à la fois simple et universel, commence à se propager hors de France. En 1875, dix-sept états signent le traité connu sous le nom de Convention du mètre, et créent le Bureau International des Poids et Mesures (BIPM: le BIPM a la charge de coordonner les travaux sur la définition des unités au niveau international ; les enjeux sont de définir des unités réalisables – par l’expérience – par tout laboratoire métrologique).
- Lors de la conférence internationale de Washington de 1884, le méridien de Greenwich fut choisi comme méridien origine. Ce méridien devint la référence internationale pour l’origine des longitudes. La Terre est alors découpée en 24 fuseaux horaires et le temps GMT (Greenwich Mean Time) voit le jour.
- Le mètre est aujourd’hui défini en fonction de la vitesse de la lumière et donc de la seconde et donc de la fréquence de la transition hyperfine du césium (toutes les unités du système international reposent désormais sur des constantes physiques : vitesse de la lumière, constante de Planck, …).
Page du site Internet du Bureau International des Poids et Mesures, https://www.bipm.org/en/home
Précisions sur la forme de la Terre
- Du fait de sa forme sphérique, le plus court chemin entre deux points à la surface de la Terre est l’arc du grand cercle qui les relie.
Google Map
- Le propos se limite ici au concept de terre sphérique mais en réalité la forme de la Terre est complexe et varie dans le temps.
- Les géodésiens font la différence entre la forme géométrique (distance entre points) et dynamique (attraction gravitationnelle entre les masses constituant la Terre). Cette nuance est essentielle pour introduire la notion d’altitude.
- Dans les années 1730 deux expéditions Françaises, l’une en Laponie, l’autre au Pérou, avaient déjà mesuré des arcs de méridiens terrestres. L’objectif n’était pas de définir le mètre mais de mesurer l’aplatissement de la Terre :
https://fr.wikipedia.org/wiki/Exp%C3%A9ditions_g%C3%A9od%C3%A9siques_fran%C3%A7aises#Les_raisons_des_exp%C3%A9ditions_fran%C3%A7aises_en_Laponie_et_en_%C3%89quateur
Existe-t-il vraiment une controverse sur la forme de la Terre ?
Bien que la forme quasi sphérique de la Terre ne fasse plus aucun doute, il se trouve toujours des personnes pour remettre en cause cette évidence : ces partisans d’une Terre plate sont les platistes. Cette croyance reste marginale mais tenace. Bien qu’elle s’appuie souvent sur des arguments qui se veulent scientifiques, elle est motivée par des considérations religieuses ou psychosociologiques (besoin d’appartenance à une communauté d’idée, paranoïa du complot, …).
Quelles que soient les motivations profondes, les arguments avancés par les platistes peuvent être analysés, décortiqués et passés au filtre de l’esprit critique des élèves. Voici quelques exemples :
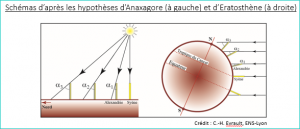
L’expérience d’Ératosthène
Contrairement à ce que l’on lit ou entend parfois, l’expérience d’Ératosthène ne constitue pas une preuve que la Terre est sphérique ; elle prend pour hypothèse que la Terre est sphérique. Cette expérience est réinterprétée par les platistes en arguant que les Soleil n’est pas très loin de la Terre et que ses rayons lumineux ne sont pas parallèles mais fortement divergents, d’où des angles d’incidence différents à des latitudes différentes sur Terre.
Si on part de l’hypothèse que la Terre est plate (hypothèse de Anaxagore), et que l’inclinaison des rayons du Soleil provient de l’angle de vue, l’expérience donne accès – par le théorème de Thalès – à la distance Terre–Soleil qui serait à alors d’environ… 6200 km.
L’alternance jour/nuit
Pour les platistes, le Soleil et la Lune sont constamment au-dessus de la Terre plate. Ce Soleil très proche et toujours au-dessus d’une Terre plate aurait un éclairement si directionnel qu’il n’éclairerait qu’une partie de la Terre à la fois. Pour expliquer l’alternance jour/nuit, ils donnent au Soleil la propriété de n’éclairer que dans un angle solide délimité, comme le ferait un projecteur. Son mouvement circulaire dans le ciel suffirait à expliquer l’alternance des jours et des nuits.
Mais il est alors très compliqué d’expliquer les variations de la durée du jour au cours de l’année, les saisons et l’équation du temps. Les platistes prennent donc quelques libertés avec la physique de base.
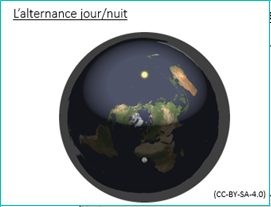
GIF : https://upload.wikimedia.org/wikipedia/commons/7/70/SunAnimation.gif
La hauteur de l’étoile polaire
L’étoile polaire nous indique la direction du Nord dans l’hémisphère Nord car elle se trouve quasiment dans la direction de l’axe de rotation de la Terre. La polaire est donc en apparence fixe dans le ciel boréal et s’observe à des hauteurs différentes dans le ciel selon la latitude du lieu. Pour les platistes, cette hauteur dans le ciel variable ne serait pas due à la rotondité de la Terre mais à un simple effet de perspective. Si tel était le cas, l’étoile polaire ne serait qu’à quelques milliers de km de la Terre. Absurde dans la mesure où d’autres mesures nous indiquent que ce n’est pas possible (parallaxe mesurée nous donnant une idée de sa distance réelle, décalage Doppler des raies de son spectre qui nous donne une idée de sa vitesse radiale, etc.).
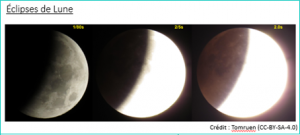
Les éclipses de Lune
Dans le modèle platiste, le Soleil et la Lune sont constamment au-dessus de la Terre plate. Si on imagine la Lune moins éloignée que le Soleil, on peut éventuellement expliquer les éclipses de Soleil. Mais quid des éclipses de Lune ? Pour les platistes, elles sont expliquées par l’existence d’un corps que les astronomes n’auraient pas découvert et qui passerait devant la Lune pour l’éclipser. Les astronomes seraient donc capables de détecter des planètes qui gravitent autour d’autre étoiles mais pas un corps céleste qui serait entre la Terre et la Lune…
Cela fait fort longtemps qu’il n’y a plus le moindre doute sur la forme sphérique de la Terre. Mais les platistes, qui ne veulent pas adhérer à des faits et théories scientifiques, qui veulent croire à une explication alternative, sont prêts à des subterfuges et malhonnêtetés intellectuelles pour parvenir à leurs fins.
Bibliographie / webographie
Cazenave et K. Feigl. Formes et mouvements de la Terre. Belin, Collection Croisée Des Sciences. 1994.Boucher.
Les références de temps et d’espace. Hermann.2017.
Eléments d’Histoire des Sciences, sous la direction de Michel Serres. Paris, Bordas. 1986.
Débarbat & A.E. Ten, éditeurs. Mètre et Système Métrique. Observatoire de Paris et Instituto de Estudios Documentales sobre la Ciencia, Universidad de Valencia. 1993.
J.J. Levallois. Mesurer la Terre : 300 ans de géodésie française, Paris, AFT, 1992.
Marquet & A. Le Bouch. L’Épopée du Mètre. Histoire du Système Métrique Décimal. Ministère de l’Industrie et de l’Aménagement du Territoire, Paris. 1989.
A.-M. Motais de Narbonne & J. Alexandre. Une mesure révolutionnaire : le mètre. Observatoire de Paris. 1988.
Deparis et H. Legros. Voyage à l’intérieur de la Terre. De la géographie antique à la géophysique actuelle. Une histoire des idées, Paris, CNRS Editions. 2000.
Site Web du Bureau International des Poids et Mesures : https://www.bipm.org
Site Web de l’Institut National de l’Information Géographique et Forestière : https://geodesie.ign.fr
Site collaboratif sur lequel des établissements scolaires peuvent déposer leurs mesures pour pouvoir refaire l’expérience d’Eratosthène avec des lieux qui conviennent : https://eratosthenes.ea.gr/
Les nouveaux croyants de la Terre plate, Religioscope, no. 42, 2018 (https://religion.info/pdf/2018_12_Mayer_TerrePlate.pdf )
Dubay, Éric, 200 preuves attestant que la Terre n’est pas une boule qui tourne, 2015 (https://www.penser-critique.be/wp-content/uploads/2020/01/200-preuves-attestant-que-la-terre-n_est-pas-une-boule-qui-tourne.pdf)
La Terre est plate et ne tourne pas, Musée des arts et métiers, Cité des sciences (http://www.cite-sciences.fr/fileadmin/_migrated/content_uploads/GRu-dossierenseignant-laterreestplate-argument_01.pdf )
AUTEURS
Jean-Charles MARTY, chercheur en géodésie spatiale au GET/Observatoire Midi-Pyrénées/CNES
Félix PEROSANZ, chercheur en géodésie spatiale au GET/Observatoire Midi-Pyrénées/CNES
Frédéric PITOUT, chercheur en astrophysique à l’IRAP/Observatoire Midi-Pyrénées/UPS
Documents associés
Journée Académique de l’Espace – 2023
La parallaxe grâce au satellite Gaia
Documents et modules pédagogiques à partir du projet SWINGS.
Mesurer l’enneigement avec son smartphone
Exemple de projet expérimental et numérique sur les microorganismes du sol
Histoire de la cristallographie
e-PERON : Plateforme Educative sur les Rayons cosmiques et les muONs
La démarche scientifique
SIGthèque académie de Toulouse
IODP France, le programme international de découverte des océans
Le saviez-vous ?
Rayons cosmiques au Pic du Midi
Activités diverses en astronomie
Rotation du ciel
Chronologie de l’Univers
Réaliser un spectroscope à CD
Réaliser un cadran solaire analemmatique
Qu’est-ce que la spectroscopie ?
Activités diverses sur l’Univers
Analyser des roches martiennes
Radiotélescope OMP
IRiS : Initiation à la Recherche en astronomie pour les Scolaires
Astrophysicien – Peter Von Ballmoos
Physicien – Jean-Michel Courty
Astrophysicien – Hervé Dole
Astrophysicien – William Lee
Chercheur-ingénieur – Nathalie Palanque
Pierre Léna, astrophysicien
Astrophysicien – Pierre Léna
Chasseur de particules cosmiques – Thierry Stolarczyk
Historien de l’astronomie – Jean-Pierre Verdet
Historien de la conquête spatiale – Jacques Villain
Météoritologue – Brigitte Zanda
Historienne des sciences – Florence Raulin-Cerceau
Mars, Curiosity et ChemCam
Histoire de la cosmologie
Pic du Midi virtuel
Comprendre la matière avec le LHC
Chercheur – Astronome
La Planeterrella
C’est pas sorcier : Géologie
Physicien de l’atmosphère – Jean-Louis Fellous
Paléo-océanographe – Yves Lancelo
Chercheur – Géophysicien
Chercheur – Minéralogiste
Festival d’astronomie de Fleurance
Découvrir l’origine des rayons cosmiques
Géolthèque Sud-Ouest
Localiser un séisme
Trajet de la lumière dans le télescope Bernard Lyot
Histoire du Pic du Midi
Enregistrer les séismes
OMER7A – POLLUTION ATMOSPHÉRIQUE : CAUSES ET CONSÉQUENCES